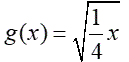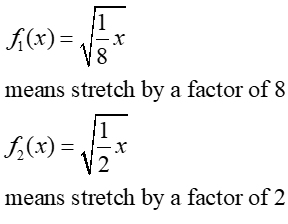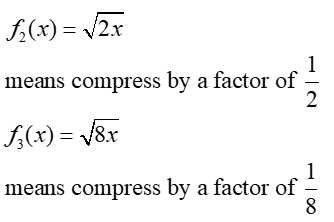Dealing with Transformations in Radical Graphs MathBitsNotebook.com Topical Outline | Algebra 2 Outline | MathBits' Teacher Resources Terms of Use   Contact Person: Donna Roberts

Transformations as they apply to Square Roots
Let's refresh what we know about transformations, and how they apply to square roots.

With the exception of the last chart section on "horizontal stretch" and "horizontal compression",
these basic transformations were studied (and can be reviewed) in Algebra 1.

Notation	Transformation Parent function:	Example	Description
- f (x)	Reflection (over x-axis)		over x-axis
f (-x)	Reflection (over y-axis)		over y-axis
f (x) + k	Vertical Shift up k units		5 units up
f (x) - k	Vertical Shift down k units		3 units down
f (x + k)	Horizontal Shift left k units		4 units left
f (x - k)	Horizontal Shift right k units		7 units right
k • f (x)	Vertical Stretch (| k | > 1)		stretch by a factor of 3
	Vertical Compress (0 < k < 1)		compress by a factor of ½
f (kx)	Horizontal Stretch (0 < k < 1)		stretch by a factor of 4
	Horizontal Compress ( | k | > 1)		compress by a factor of ½

While these examples list only square roots, these transformations also apply to cube roots, and other radical functions.

The generic graphical formulas for square roots and cube roots,
that emphasize transformations, are:

Square root:

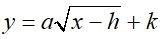Cube root:

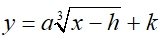Let's start by examining a reflection over the y-axis, because at first glance,
that formula looks really confusing! A negative under the radical?

The clue to what is happening is in examining what happens as we move along the x-axis.

x	-16	-9	-4	-1	0	1	4	9	16
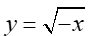	4	3	2	1	0	not real	not real	not real	not real
Graph	(-16,4)	(-9,3)	(-4.2)	(-1,1)	(0,0)	None	None	None	None

As long as the domain stays negative (or zero), there is no problem.
We have real numbers that can be graphed.

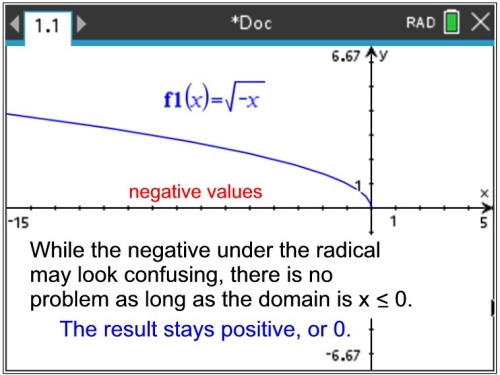
The end behavior for this graph is
 as x → 0^-,  f (x) → 0 (comes from the left)    and    as x → -∞,  f (x) → +∞

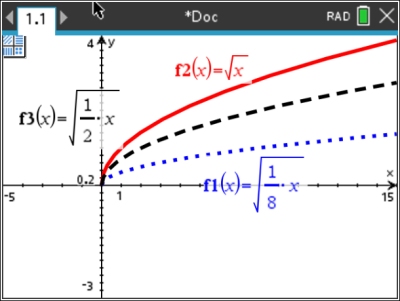
As was stated above, the last section of the chart was most likely not covered in Algebra 1.
Therefore, a lesson has been devoted to "Horizontal Stretch or Compress".
If you have not seen this transformation in action, please take a look before continuing.

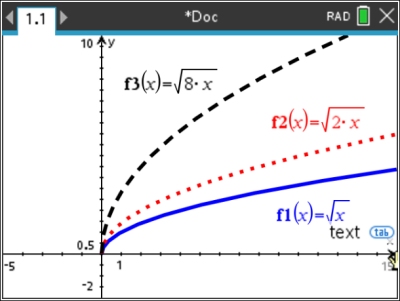
Horizontal Stretch       (f (k•x) where 0 < k < 1)

Parent function: The smaller the fraction constant, the further the pull away from the y-axis.

A horizontal stretch "pulls" the graph horizontally away from the y-axis
(to the left and/or right).

Horizontal Compression       (f (k•x) where k > 1)

Parent function: The larger the constant in front of x, the closer the push toward the the y-axis.

A horizontal compression "pushes" the graph horizontally closer to the y-axis
(to the left and/or right).

For calculator help with graphing radical functions. click here.

Topical Outline | Algebra 2 Outline | MathBitsNotebook.com | MathBits' Teacher Resources
Terms of Use    Contact Person: Donna Roberts